Komplexität der Corona-Fallzahlen

Einführung in die Theorie komplexer Systeme - Corona.Verbreitung

Mit Hilfe der Komplexitätsforschung lässt sich die Stabilität und damit die Vorhersagbarkeit eines Systems bestimmen. Die Zahl der erkrankten Personen in Wien zeigte zunächst eine hohe Komplexität. Ohne einschränkende Maßnahmen verbreitet sich das Virus sehr schnell. Gleichzeitig liegen zu Beginn aber auch nur wenige Fälle vor und in so einer Situation ist keineswegs klar, wie sich die Verbreitung weiter entwickelt. Die Krise startet also mit großer Unsicherheit (Komplexität).

Komplexitätsmessungen können Veränderungen in Systemen vorhersagen. Darauf wurde unten schon mehrfach hingewiesen.

Analyse

Mit Hilfe der Komplexitätsforschung lässt sich die Stabilität und damit die Vorhersagbarkeit eines Systems bestimmen. Die Zahl der erkrankten Personen in Wien zeigte zunächst eine hohe Komplexität. Ohne einschränkende Maßnahmen verbreitet sich das Virus sehr schnell. Gleichzeitig liegen zu Beginn aber auch nur wenige Fälle vor und in so einer Situation ist keineswegs klar, wie sich die Verbreitung weiter entwickelt. Die Krise startet also mit großer Unsicherheit (Komplexität). Aber schon nach wenigen Tagen hat sich die dramatische Verbreitung (simples exponentielles Wachstum) durchgesetzt. Das System verhält sich jetzt geordnet. Ein Zustand, der in diesem Fall keinesfalls angenehm ist. Das System verhält sich so einfach und geordnet, dass sich die Dramatik der Verbreitung leicht mit einem einfachen Taschenrechner vorhersagen lässt.

Ohne drastische Gegenmaßnahmen ist eine solche Entwicklung in kurzer Zeit nicht mehr zu stoppen. Das die Maßnahmen wirken zeigt sich dann auch. Die Kurve flacht ab und das System zeigt erneut einen starken Anstieg der Komplexität. Auch hier ist das der Hinweis darauf, dass sich das Systemverhalten in Kürze ändern wird, was auch tatsächlich der Fall war.

Komplexitätsmessungen können Veränderungen in Systemen vorhersagen. Darauf wurde unten schon mehrfach hingewiesen. Ein Forschungsantrag unseres Instituts für ein solches Vorhersagesystem ist leider nicht gefördert worden. Frühwarnsysteme für Krisen waren anscheinend nicht gefragt.

Analyse

Die Fallzahlen in Wien fluktuieren. Diese Trend zur höheren Komplexität hatte sich bereits abgezeichnet So war die Komplexität in den letzten Tagen recht hoch. Dies kann ein Vorwarnsignal für Veränderungen sein. Die folgende Abbildung zeigt die neuen Analyse. Die Methoden werden weiter unten in vorherigen Posts beschrieben.

Analyse

Große Veränderungen sind für die Fallzahlen in Wien nicht sichtbar. Dennoch war die Komplexität in den letzten Tagen recht hoch. Dies kann ein Vorwarnsignal für Veränderungen sein. Die folgende Abbildung zeigt die neuen Analyse. Die Methoden werden weiter unten in vorherigen Posts beschrieben.

Analyse

Derzeit zeigen sich in Wien keine grundlegenden Veränderungen in der Dynamik. Die folgende Abbildung zeigt die neuen Analyse. Die Methoden werden weiter unten in vorherigen Posts beschrieben.

Analyse

Eines der berühmtesten und am meisten verwendete Maße zur Bestimmung von Komplexität ist die fraktale Dimension. Konkret kann die mit dem sog. D2 Kennwert bestimmt werden. Eine Erweiterung der Methode kann für jeden Zeitpunkt die fraktale Dimension bestimmen benötigt dafür aber insgesamt recht viele Zeitpunkte mit Daten. Je höher die fraktale Dimension, desto höher ist die Komplexität.

Eigentlich ist der Datensatz noch recht kurz für dieses Verfahren, aber die Berechnung gelingt und bestätigt die bisherigen Ergebnisse: Immer dann, wenn das System sein Verhalten ändert steigt die Komplexität an. Diesen Effekt kennen wir aus der Theorie der Synergetik. Frühwarnsysteme für plötzliche Veränderungen lassen sich aus diesen Überlegungen ableiten (Siehe dazu auch hier).

Es folgen die Auswertungen für die Daten aus Wien (Daten). Die Grafiken beziehen sich auf die Zahl der aktuell erkrankten Personen (blaue Punkte). Einige Methoden und theoretische Überlegungen wurden bereits vor einigen Tagen bzw. Wochen diskutiert und finden sich daher weiter unten.

Analyse

Analyse

Die Synergetik ist eine der bedeutsamsten Komplexitätstheorien. Sie sagt voraus, dass die Komplexität eines Systems viel über seine Stabilität verrät. Steigt die Komplexität plötzlich sprunghaft an, dann kann das eine bedeutsame Verhaltensänderung im System anzeigen. Mitunter gelingt damit bereits eine Vorwarnung für zukünftige Verhaltensänderungen.

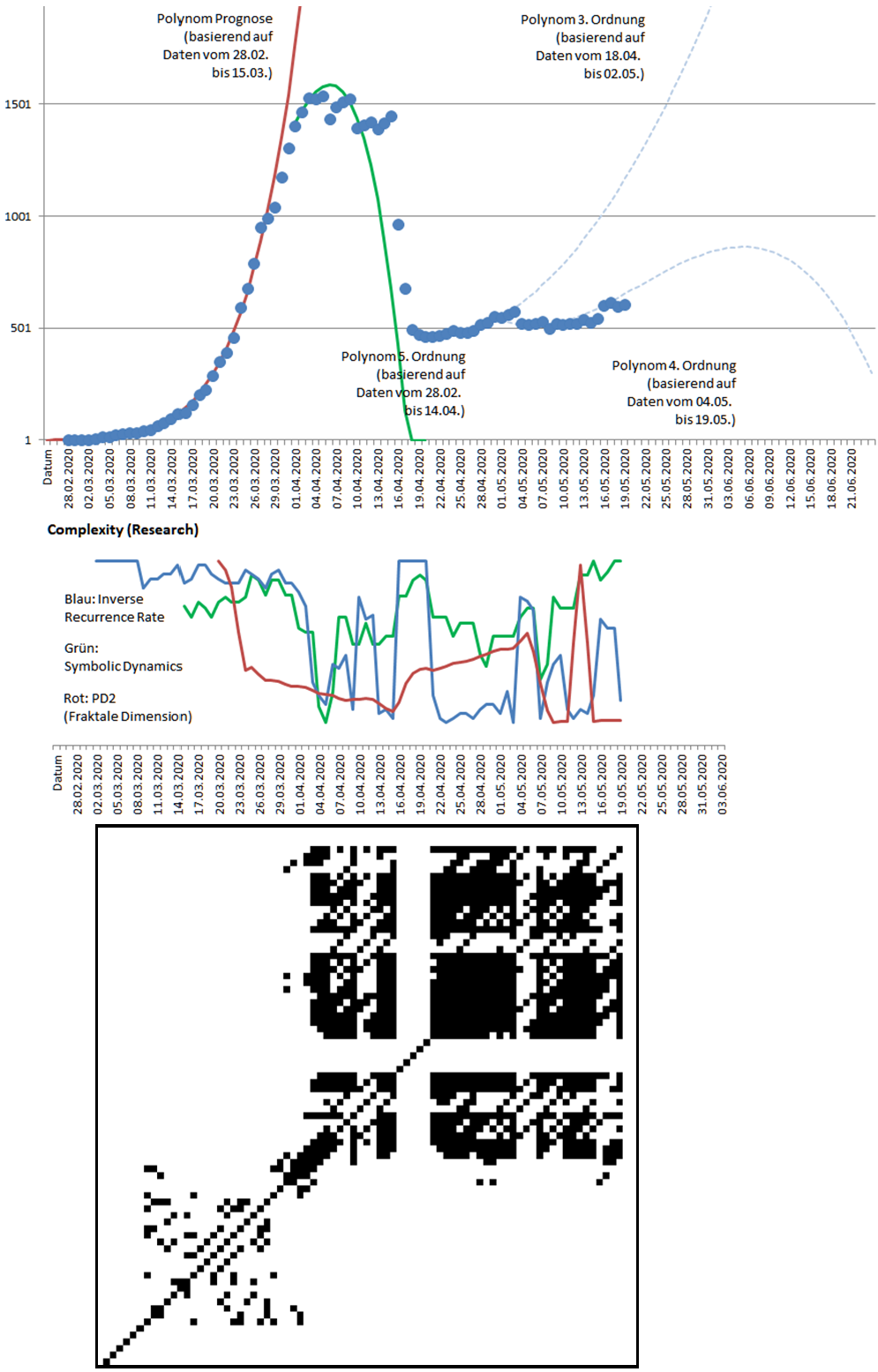
Das Problem besteht darin die Komplexität des Systemverhaltens zu messen. Denn dafür sind recht große Datenmengen (lange Zeitreihen) nötig. Versucht man es mit weniger reliablen Methoden, können auch kurze Zeitreihen genügen aber die Ergebnisse sind ungenau. In den bisherigen Analysen wurde eine Methode aus dem Bereich der Symbolic Dynamics benutzt. Damit war in den letzten Tagen ein Anstieg der Komplexität zu sehen, der den Rückgang der Fallzahlen für Wien zugeordnet werden kann.

Auch Recurrence Plots verraten viel über die Komplexität eines Systems. Wiederkehrende Zustände werden in diesen Abbildungen schwarz markiert. Dieses Verfahren zeigt noch einmal deutlicher dramatische Veränderungen in der Komplexität. Das Verfahren und erste Ergebnisse wurden bereits auf dieser Seite präsentiert.

Der Beginn der Krise ist gekennzeichnet durch eine maximale Komplexität. Das System beginnt sich einzupendeln auf ein exponentielles Wachstum. In dieser Phase ist es erschreckend leicht vorhersagbar. Die Komplexität geht daher runter. Ein sprunghafter Anstieg der Komplexität ist ab dem 12.04. sichtbar und dauert bis zum 17.04. Dieser Anstieg der Komplexität zeigt die Veränderung des Systemverhaltens (Rückgang der Erkrankungen) deutlich an. Seit dem ist die Komplexität wieder gering. Das System scheint vorhersagbar zu sein und verändert sich wenig.

Analyse

24.04.2020

Analyse

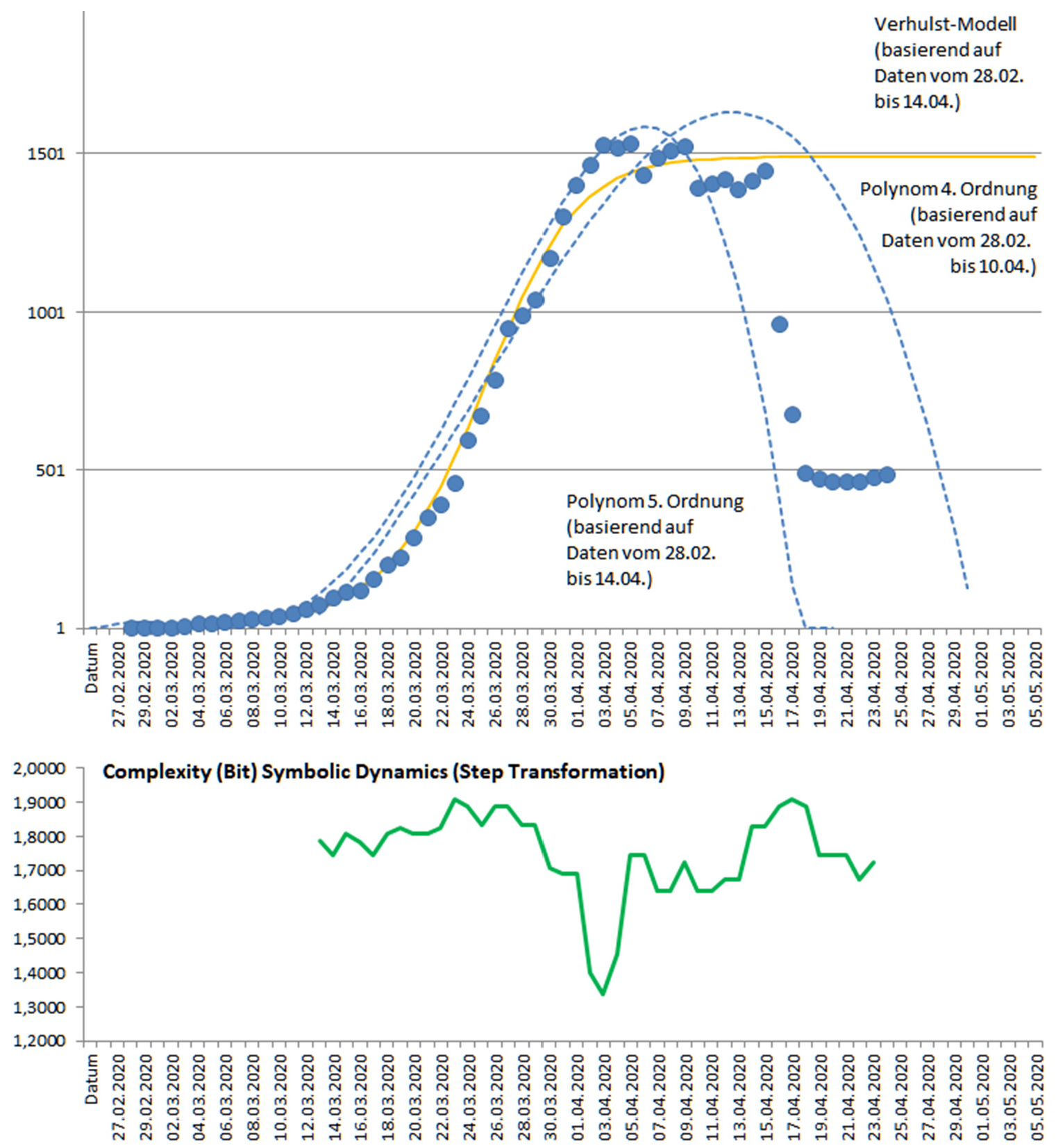
Die folgende Abbildung wurde für Wien erstellt. Die Zeitreihe zeigt die Zahl der jeweils erkrankten Personen. Polynomanpassungen und das aus der Komplexitätsforschung bekannte Verhulst-System (siehe: Therapeutisches Chaos, Systemische Psychologie, Komplexe Welt) modellieren die Daten und geben einen Eindruck möglicher zukünftiger Entwicklungen.

Analyse

Die Zahlen gehen herunter!

Die folgende Abbildung wurde für Wien erstellt. Die Zeitreihe zeigt die Zahl der jeweils erkrankten Personen. Polynomanpassungen und das aus der Komplexitätsforschung bekannte Verhulst-System (siehe: Therapeutisches Chaos, Systemische Psychologie, Komplexe Welt) modellieren die Daten und geben einen Eindruck möglicher zukünftiger Entwicklungen.

Die Komplexitätsberechnung zeigt jüngst einen Anstieg der Komplexität. Dies kann ein Zeichen für eine Veränderung des Systemverhaltens sein.

Analyse

Die folgende Abbildung wurde für Wien erstellt. Die Zeitreihe zeigt die Zahl der jeweils erkrankten Personen. Polynomanpassungen und das aus der Komplexitätsforschung bekannte Verhulst-System (siehe: Therapeutisches Chaos, Systemische Psychologie, Komplexe Welt) modellieren die Daten und geben einen Eindruck möglicher zukünftiger Entwicklungen.

Die Komplexitätsberechnung zeigt jüngst einen Anstieg der Komplexität. Dies kann ein Zeichen für eine Veränderung des Systemverhaltens sein.

Analyse

Die folgende Abbildung wurde für Wien erstellt. Die Zeitreihe zeigt die Zahl der jeweils erkrankten Personen. Polynomanpassungen und das aus der Komplexitätsforschung bekannte Verhulst-System (siehe: Therapeutisches Chaos, Systemische Psychologie, Komplexe Welt) modellieren die Daten und geben einen Eindruck möglicher zukünftiger Entwicklungen.

Die Komplexitätsberechnung zeigt jüngst einen Anstieg der Komplexität. Dies kann ein Zeichen für eine Veränderung des Systemverhaltens sein.

Analyse

Die folgende Abbildung wurde für die Fallzahlen für Wien erstellt. Die Zeitreihe zeigt die Zahl der jeweils aktuell erkrankten Personen. Polynomanpassungen und das aus der Komplexitätsforschung bekannte Verhulst-System (siehe: Therapeutisches Chaos, Systemische Psychologie, Komplexe Welt) modellieren die Daten und geben einen Eindruck möglicher zukünftiger Entwicklungen.

Die Komplexitätsberechnung zeigt jüngst einen Anstieg der Komplexität. Dies kann ein Zeichen für eine Veränderung des Systemverhaltens sein.

Analyse

Komplexität kann bei etwas längeren Zeitreihen recht gut über klassische Verfahren der Informationsdefinition bestimmt werden. Es geht dabei darum in der Zeitreihe bevorzugte Muster zu finden. Ein Würfel zeigt keine bevorzugten Muster. Die gewürfelten Zahlen verhalten sich maximal komplex. Geordnete Systeme zeigen hingegen Muster, die sich wiederholen. Die folgende Abbildung zeigt zunächst die Entwicklung der Fallzahlen für Wien und darunter die Komplexität für eine Abfolge von drei Tagen und einer Beobachtungszeit von 14 Tagen. Es werden also innerhalb von 14 Tagen sich wiederholende 3er-Muster gesucht. Das 14 Tage-Fenster wird nach und nach über den gesamten Datensatz geschoben. Dabei zeigen sich mal mehr und mal weniger dominante Muster. Die Komplexität geht auf und ab.

Theoretische Ansätze sagen dort ein Anwachsen der Komplexität voraus, wo es zu einer Veränderung des Systemverhaltens kommt. Das war zu Beginn der Krise der Fall und Ende März und den ersten Apriltagen.

Analyse

Bifurkationspunkte heißen in der Komplexitätsforschung Verzweigungen im Systemverhalten. Das System steht hier auf Messers Schneide und es ist nicht möglich vorherzusagen wohin es sich bewegen wird. Die aktuellen Daten für Wien zeigen entweder weiter nach oben oder einen deutlichen Rückgang.

Analyse

Analyse

Komplex ist ein System, dessen Verhalten sich prinzipiell nicht vorhersagen lässt, obwohl eigentlich alle relevanten Informationen über das System vorhanden sind. Umgekehrt ist ein System, welches über einen hohen Anteil wiederkehrender Muster verfügt wenig komplex. Wiederkehrende Muster sind ein Zeichen für Ordnung. Ein einfaches Verfahren der Komplexitätsforschung markiert Zeitpunkte in einer Grafik, die sich zu anderen Zeiten ähnlich ereignet haben. Wenn also der gleiche/ähnliche Messwert zu zwei Zeitpunkten vorlag, wird dies in der Grafik mit einem schwarzen Punkt markiert. Solche Abbildungen heißen Recurrence  Plots (Wiederkehr-Abbildungen). Die Muster, der schwarzen Punkte verraten viel über die die Komplexität und die Stabilität des Systems. Dort wo sie sich häufen war der System geordnet. Dort, wo sie fehlen war es komplex. Die folgende Abbildung zeigt den Recurrence Plot für die täglichen Zuwachsraten der Corona Ausbreitung in Wien. Zu Beginn fehlen schwarze Punkte. Das System ist hoch komplex und hat sich noch nicht auf ein Muster eingestellt.

Der Recurrence Plot für die täglichen Zuwachsraten der Corona Ausbreitung in Wien zeigt zunächst keine wiederkehrenden Zeitpunkte. Ca. ab dem 08.03. bauen sich wiederkehrende Muster auf. Die Zahl der schwarzen Punkte nimmt zu. Die Zuwachsraten sind vorhersagbar und wenig komplex. Zwischen dem 27.03. und den 31.03. kommt es zu einem Bruch mit höherer Komplexität (weißer Bereich), der in einen schwarzen Block übergeht. Hier liegen die Zuwachsraten dicht beisammen und sind einander sehr ähnlich. (Technische Details: 3-dimensionale Phasenraumeinbettung mit einem Time-Lag von 1 und einer Recurrence Rate von RR = 0,2.)

Immer mehr Modelle sehen ein Ende der Krise voraus. Aber derzeit sind die Modelle noch sehr unsicher. Ein Polynom (5. Ordnung, basierend auf allen verfügbaren Daten für Wien) prognostiziert eine baldige Abnahme, ist aber sicherlich zu optimistisch. Auch ein Verhulst-System lässt an die bisherigen Daten anpassen und zeigt ein Plateau ab Mitte April. Beide Modell bemühen sich die verringerten Zuwächse der letzten Woche abzubilden. Ob dieser positive Trend hält lässt sich noch nicht absehen.
Komplexitätsforschung: Die grüne Kurve zeichnet den Verlauf der Komplexität der Daten nach. Das System war zu Beginn wenig geordnet und hat sich dann schnell stabilisiert. Eine Verhaltensänderung würde laut Theorie erneut zu einer Destabilisierung mit erhöhter Komplexität führen. Das ist bislang nicht zu sehen. Auch das Verhulst-Modell ist ein Modellsystem der Komplexitätsforschung und das bekannteste zu Chaos / Komplexität fähige Simulationsmodell. (Siehe: Therapeutisches Chaos, Systemische Psychologie, Komplexe Welt).

Analyse

Immer mehr Modelle sehen ein Ende der Krise voraus. Aber derzeit sind die Modelle noch sehr unsicher. Ein Polynom (5. Ordnung, basierend auf allen verfügbaren Daten für Wien) prognostiziert eine baldige Abnahme, ist aber sicherlich zu optimistisch. Auch ein Verhulst-System lässt an die bisherigen Daten anpassen und zeigt ein Plateau ab Mitte April. Beide Modell bemühen sich die verringerten Zuwächse der letzten Woche abzubilden. Ob dieser positive Trend hält lässt sich noch nicht absehen.
Komplexitätsforschung: Die grüne Kurve zeichnet den Verlauf der Komplexität der Daten nach. Das System war zu Beginn wenig geordnet und hat sich dann schnell stabilisiert. Eine Verhaltensänderung würde laut Theorie erneut zu einer Destabilisierung mit erhöhter Komplexität führen. Das ist bislang nicht zu sehen. Auch das Verhulst-Modell ist ein Modellsystem der Komplexitätsforschung und das bekannteste zu Chaos / Komplexität fähige Simulationsmodell. (Siehe: Therapeutisches Chaos, Systemische Psychologie, Komplexe Welt).

Analyse

  Am 15.03. habe ich an die bis dahin vorliegenden Daten für Wien ein Polynom angepasst. Der Verlauf war/ist gemäßigter als der einer Exponentialfunktion durch die gleichen Daten. Die Daten der letzten Tage entwickeln sich positiver als vermutet. Ein Polynom (6. Ordnung) prognostiziert daher eine baldige Abnahme, ist aber sicherlich zu optimistisch. Ein Verhulst-System lässt sich perfekt an die bisherigen Daten anpassen und zeigt ein Plateau ab Mitte April. Beide Modell bemühen sich die geringen Fallzahlen des letzten Wochenendes einzufangen und kommen daher wahrscheinlich zu einer zu optimistischen Schätzung.
Komplexitätsforschung: Die grüne Kurve zeichnet den Verlauf der Komplexität der Daten nach. Das System war zu Beginn wenig geordnet und hat sich dann schnell stabilisiert. Eine Verhaltensänderung würde laut Theorie erneut zu einer Destabilisierung mit erhöhter Komplexität führen. Die neuen Daten lassen die Kurve minimal ansteigen. Das Verhulst-Modell ist ein Modellsystem der Komplexitätsforschung und das bekannteste zu Chaos / Komplexität fähige Simulationsmodell. (Siehe: Therapeutisches Chaos, Systemische Psychologie, Komplexe Welt).

Analyse

Analyse

Die Anpassung eines exponentiellen Modells an die Fallzahlen der Corona.Verbreitung in Wien ist einfach. Aber ein exponentielles Modell kann einzig das Wachstum abbilden. Da es in solch einem Modell immer nur nach Oben geht, ist ein Ende nicht absehbar. Das Ende der Krise ist nicht Teil des Modells.

Man benötigt also andere Modellannahmen, um das Erreichen eines Maximums und ein anschließendes Sinken der Erkrankungen überhaupt abbilden zu können. Ein solches Modell könnte ein Polynom höherer Ordnung sein. Allerdings kann die Prognose eines Polynoms dramatisch danebenliegen, wenn man zu weit damit in die Zukunft schaut.

Unten hatte ich zudem ein Verhulst-Modell vorgestellt. Es handelt sich um ein seit 1844 gebräuchliches Modell, um Wachstumsprozesse zu modellieren. Neben einem exponentiellen Wachstum wird auch der Rückgang der Erkrankungen berücksichtigt. Das Verhulst-Modell für die aktuellen Daten zeigt noch keinen Rückgang aber bereits das Erreichen eines Plateaus an.

Noch wirken sich die geringen Fallzahlen des Wochenendes aus.

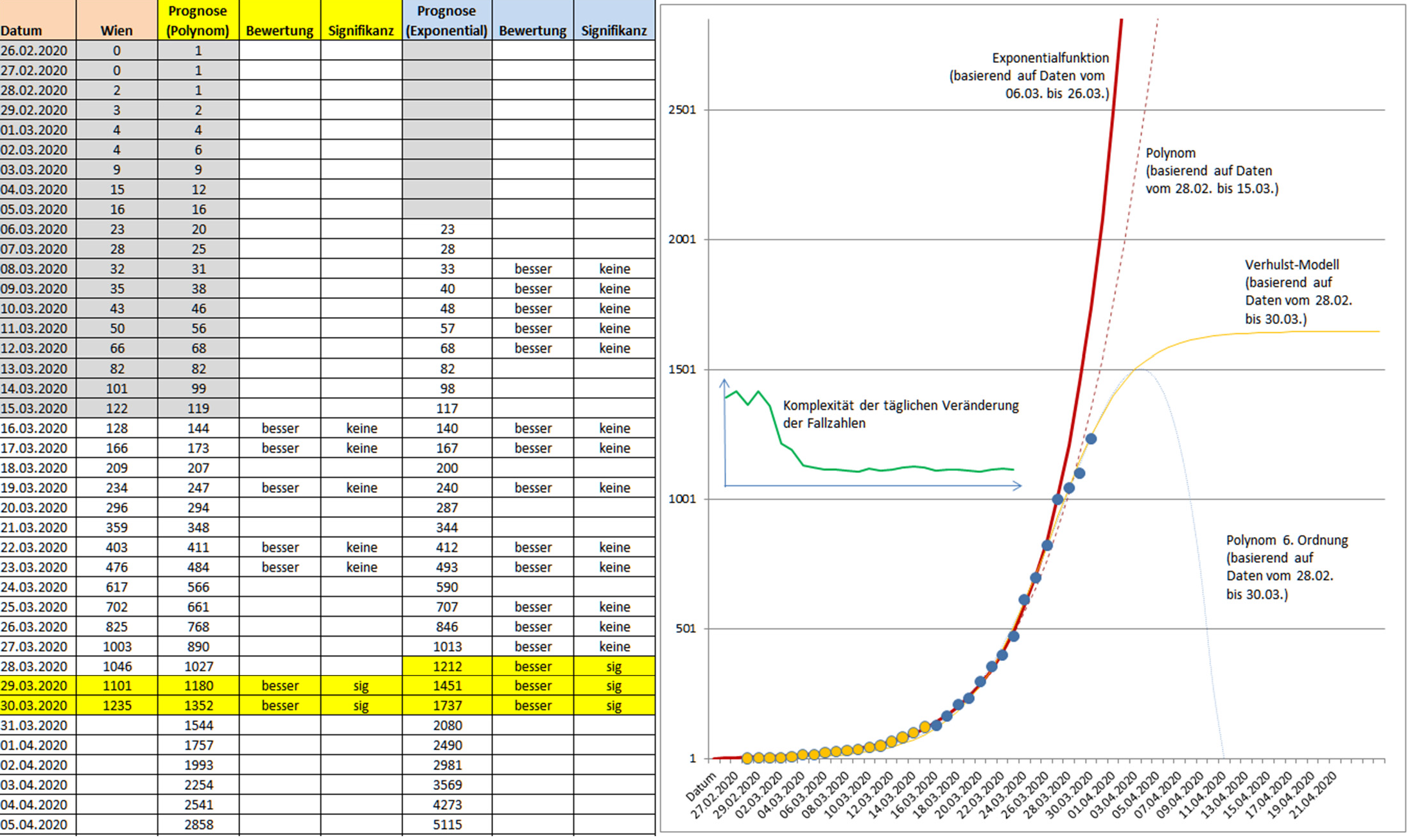
Am 15.03. habe ich an die bis dahin vorliegenden Daten für Wien ein Polynom angepasst. Der Verlauf war/ist gemäßigter als der einer Exponentialfunktion durch die gleichen Daten. Dieses Polynom hat bis zum 23.03. auch tatsächlich besser zu den Daten gepasst. Danach hat sich der Verlauf beschleunigt und das Polynom hat die Fallzahlen deutlich unterschätzt. Daher habe ich anstelle des Polynoms eine Exponentialfunktion für die Daten zwischen dem 06.03 und dem 26.03. angepasst. Diese war einige Tage bestimmend. Die Daten der letzten Tage entwickeln sich aber deutlich positiver. Ein Polynom (6. Ordnung) prognostiziert eine baldige Abnahme, ist aber sicherlich zu optimistisch. Ein Verhulst-System lässt sich perfekt an die bisherigen Daten anpassen und zeigt ein Plateau ab Mitte April. Beide Modell bemühen sich die geringen Fallzahlen des Wochenendes einzufangen und kommen daher wahrscheinlich zu einer zu optimistischen Schätzung.
Komplexitätsforschung: Die grüne Kurve zeichnet den Verlauf der Komplexität der Daten nach. Das System war zu Beginn wenig geordnet und hat sich dann schnell stabilisiert. Eine Verhaltensänderung würde laut Theorie erneut zu einer Destabilisierung mit erhöhter Komplexität führen. Die neuen Daten lassen die Kurve minimal ansteigen. Das Verhulst-Modell ist ein Modellsystem der Komplexitätsforschung und das bekannteste zu Chaos / Komplexität fähige Simulationsmodell. (Siehe: Therapeutisches Chaos, Systemische Psychologie, Komplexe Welt).

Analyse

Erneut gibt es in Wien geringere Zuwächse als mit dem einfachen Prognosemodell (exponentielles Modell) zu erwarten wäre. Das sind gute Nachrichten.

Am 15.03. habe ich an die bis dahin vorliegenden Daten für Wien ein Polynom angepasst. Der Verlauf war/ist gemäßigter als der einer Exponentialfunktion durch die gleichen Daten. Dieses Polynom hat bis zum 23.03. auch tatsächlich besser zu den Daten gepasst. Danach hat sich der Verlauf beschleunigt und das Polynom hat die Fallzahlen stark unterschätzt. Daher habe ich anstelle des Polynoms eine Exponentialfunktion für die Daten zwischen dem 06.03 und dem 26.03. angepasst. Diese war einige Tage bestimmend. Die Daten der letzten beiden Tage entwickeln sich aber deutlich positiver. Ein Polynom (6. Ordnung) prognostiziert eine baldige Abnahme, beruht aber auf den erfreulich geringen Fallzahlen für heute und gestern (29.03. und 28.03.). Dabei handelt es sich wahrscheinlich, um eine verzögerte Datenaktualisierung (LINK). Oder, gibt es tatsächlich Grund zum Aufatmen?
Komplexitätsforschung: Die grüne Kurve zeichnet den Verlauf der Komplexität der Daten nach. Das System war zu Beginn wenig geordnet und hat sich dann schnell stabilisiert. Eine Verhaltensänderung würde laut Theorie erneut zu einer Destabilisierung mit erhöhter Komplexität führen. Die neuen Daten lassen die Kurve minimal ansteigen.

Analyse

Polynome sind flexible Werkzeuge die sich auch an erratische Daten anpassen lassen (siehe hier). Heute gibt es erstaunlich wenig neue Fälle in Wien und ich habe ein neues Polynom angepasst. Danach wäre es bald geschafft. Aber die geringe Zahl heute um 15.00 Uhr ist wahrscheinlich nicht valide. Schade. Schauen wir, wie es weiter geht.

Am 15.03. habe ich an die bis dahin vorliegenden Daten für Wien ein Polynom angepasst. Der Verlauf war/ist gemäßigter als der einer Exponentialfunktion durch die gleichen Daten. Dieses Polynom hat bis zum 23.03. auch tatsächlich besser zu den Daten gepasst. Inzwischen scheint das Polynom die Fallzahlen zu unterschätzen. Eine neue Prognose beruht auf einer Exponentialfunktion, die für die Daten zwischen dem 06.03 und dem 26.03. angepasst wurde. Das neue Polynom (5. Ordnung) prognostiziert eine baldige Abnahme, beruht aber auf der geringen Fallzahl für heute (28.03.). Dabei handelt es sich wahrscheinlich um eine verzögerte Datenaktualisierung.
Komplexitätsforschung: Die grüne Kurve zeichnet den Verlauf der Komplexität der Daten nach. Das System war zu Beginn wenig geordnet und hat sich dann schnell stabilisiert. Eine Verhaltensänderung würde laut Theorie erneut zu einer Destabilisierung mit erhöhter Komplexität führen.

Analyse

Komplexe Systemen werden unglaublich komplex, bevor sich etwas verändert. Der Beginn der Krise hat sich durch eine hohe Komplexität ausgezeichnet. Ein erneutes Ansteigen der Komplexität kann bedeuten, dass sich das System auf ein neues - hoffentlich besseres - Muster einstellt.

Am 15.03. habe ich an die bis dahin vorliegenden Daten für Wien ein Polynom angepasst. Der Verlauf war/ist gemäßigter als der einer Exponentialfunktion durch die gleichen Daten. Dieses Polynom hat bis zum 23.03. auch tatsächlich besser zu den Daten gepasst. Inzwischen scheint das Polynom die Fallzahlen deutlich zu unterschätzen. Eine neue Prognose beruht auf einer Exponentialfunktion, die für die Daten zwischen dem 06.03 und dem 26.03. angepasst wurde.
Komplexitätsforschung: Die grüne Kurve zeichnet den Verlauf der Komplexität der Daten nach. Das System war zu Beginn wenig geordnet und hat sich dann schnell stabilisiert. Eine Verhaltensänderung würde laut Theorie erneut zu einer Destabilisierung mit erhöhter Komplexität führen.

Analyse

Komplexe Systemen werden unglaublich komplex, bevor sich etwas verändert. Der Beginn der Krise hat sich durch eine hohe Komplexität ausgezeichnet. Ein erneutes Ansteigen der Komplexität kann bedeuten, dass sich das System auf ein neues - hoffentlich besseres - Muster einstellt. (Siehe dazu auch hier.)

Die aktuellen Daten für Wien zeigen erneut ungünstige Abweichungen von der Prognose, die ich am 15.03. erstellt habe (Polynom). Ein aktuelles Exponentialmodell passt besser, was aber eben keine Verbesserung wäre. Noch weichen die Daten der letzten 14 Tage nicht signifikant von den Prognosemodelle ab.

Ich möchte noch einmal darauf hinweisen, dass ein zusammenfassendes Bild für ganz Österreich nicht funktionieren kann. Verbesserungen in dem einen Bundesland können Verschlechterungen in einem anderen ausgleichen. Die einzelnen Bundesländer sind sehr verschieden betroffen, unterschiedlich dicht besiedelt und von unterschiedlichen Maßnahmen betroffen. Exemplarisch poste ich hier Entwicklungen in Wien.

Die orangenen Punkte wurden für die Modellanpassung des Polynoms benutzt. Das Polynom beruht also auf Daten bis zum 15.03. Die dunkelrote Kurve durch diese Punkte wird verlängert (Prognose). Die blauen Punkte zeigen die tatsächlichen Fallzahlen. Die Daten sind die jeweils gegen 15 Uhr veröffentlichten Zahlen (LINK). Ein einfacher exponentieller Verlauf wurde zudem für alle bisher vorliegenden Daten angepasst. Er verläuft steiler als das Polynom. Da das Exponentialmodell neuere Daten berücksichtigt passt es auch besser. Das alleine ist also kein Wunder. Ungünstig ist aber, dass es einen steileren Verlauf zeigt.
Komplexitätsforschung: Die grüne Kurve zeichnet den Verlauf der Komplexität der Daten nach. Das System war zu Beginn wenig geordnet und hat sich dann schnell stabilisiert. Eine Verhaltensänderung würde laut Theorie erneut zu einer Destabilisierung mit erhöhter Komplexität führen.

Analyse

Komplexe Systeme verhalten sich unvorhersehbar. Das ist es, was sie als komplexe Systeme auszeichnet.

Die Synergetik ist eine der einflussreichsten Komplexitätstheorien. Sie wurde zunächst entwickelt um Selbstorganisationsprozesse im Laser zu erklären und dann auf verschiedene andere Bereiche der belebten und unbelebten Natur übertragen. Unten wurden schon dargestellt, wie ein zunächst ungeordnetes System durch Selbstorganisationsprozess erst allmählich und dann lawinenartig beschleunigt in ein "geordnetes" Verhalten übergeht. Die Synergetik sagt für Systeme - wie sie bei der Verbreitung eines Virus vorliegen könnten - voraus, dass sie sich zunächst ungeordnet verhalten und dann zunehmend in den Sog der Selbstorganisation geraten. Sie sollten zu Beginn hoch komplex sein. Das ist durchaus plausibel. Sind erst wenige Fälle gegeben, dann kann das System sich auch noch anders entwickeln. Geht die erste infizierte Person nicht mehr vor die Tür, dann kann die Geschichte hier schon enden. Erst wenn immer mehr Fälle dazu kommen, ist die Lawine ohne drastische Maßnahmen nicht mehr aufzuhalten. Zu Beginn ist noch alles offen; danach wird die Beeinflussung des Systems sehr viel schwerer.

Messungen der Komplexität von Zeitreihendaten sind heute durchaus möglich und üblich. Z.B. messen moderne Sportuhren die Komplexität der Herzfrequenz und bestimmen daraus den Fitnesslevel von Sportlerinnen und Sportlern. Für die Messung der Komplexität in kurzen Datenreihen haben Schiepek und Strunk ein Verfahren vorgeschlagen (Dynamische Komplexität). Wendet man dieses Verfahren auf die Veränderungsraten der Corona-Fallzahlen für Wien an, so zeigt sich der Übergang von der Unordnung zur Ordnung sehr deutlich: Zunächst ist das System hoch komplex und dann nur mehr erschreckend einfach vorhersagbar.

Die Synergetik geht davon aus, dass sich eine neuerliche Veränderung des Systemverhaltens erneut durch eine Komplexitätserhöhung ankündigt. Wir werden sehen.

Zu Beginn des letzten Jahres haben wir ein Forschungsprojekt bei der FFG eingereicht, um mit den Methoden der Komplexitätsforschung "Frühwarnsysteme für Krisen" zu entwickeln (Kurzversion des Antrags). Das Projekt wurde nicht für förderwürdig befunden. Wer braucht schon Methoden zur Vorhersage von Krisen?

Die orangenen Punkte wurden für die Modellanpassung des Polynoms benutzt. Die dunkelrote Kurve durch diese Punkte wird verlängert. Die blauen Punkte zeigen die tatsächlichen Fallzahlen. Die Daten sind die jeweils gegen 15 Uhr veröffentlichten Zahlen (LINK). Ein einfacher exponentieller Verlauf wurde zudem für alle bisher vorliegenden Daten angepasst. Er verläuft steiler als das Polynom. Die grüne Kurve zeichnet den Verlauf der Komplexität der Daten nach. Das System war zu Beginn wenig geordnet und hat sich dann schnell stabilisiert. Eine Verhaltensänderung würde laut Theorie erneut zu einer Destabilisierung mit erhöhter Komplexität führen.

Analyse

Komplexe Systeme verhalten sich unvorhersehbar. Das ist es, was sie als komplexe Systeme auszeichnet.

Am 15.03. - also noch vor Einführung der Maßnahmen - habe ich ein einfaches Polynom an die bis dahin vorliegenden Daten angepasst (siehe unten). Dieses Modell hat immer noch Gültigkeit. Eine Verbesserung durch die Maßnahmen ist derzeit noch nicht erkennbar. Die heutigen Daten liegen sogar deutlich über der Schätzung. Insgesamt ist die Verbreitung des Corona Virus in Wien immer noch erschreckend einfach vorherzusagen. Das Systemverhalten ist derzeit leider nicht komplex.

Die orangenen Punkte wurden für die Modellanpassung benutzt. Die rote Kurve durch diese Punkte wird verlängert. Die blauen Punkte zeigen die tatsächlichen Fallzahlen. Die Daten sind die jeweils gegen 15 Uhr veröffentlichten Zahlen (LINK).

Analyse

Komplexe Systeme verhalten sich unvorhersehbar. Das ist es, was sie als komplexe Systeme auszeichnet. Die Verbreitung des Corona-Virus ist hingegen immer noch erschreckend einfach vorherzusagen.

Die orangenen Punkte wurden für die Modellanpassung benutzt. Die rote Kurve durch diese Punkte wird verlängert. Die blauen Punkte zeigen die tatsächlichen Fallzahlen. Die Daten sind die jeweils gegen 15 Uhr veröffentlichten Zahlen (LINK).

Prognosen und deren Zuverlässigkeit sind ein zentraler Forschungsgegenstand der Komplexitätsforschung. Prognosen über die zeitliche Entwicklung eines Systems können mit verschiedenen Methoden erstellt werden:

Ein konkretes Modell ist bereits bekannt: Wachstums und Vermehrungsprozesse werden seit Mitte des 19. Jahrhunderts mit einfachen mathematischen Modellen beschrieben. Das sog. Verhulst-Modell - es wurde bereits um 1844 von Pierre François Verhulst vorgeschlagen - setzt sich aus zwei simplen Funktionsteilen zusammen. Der eine beschreibt die Vermehrung und die andere den Rückgang. Die Vermehrung wird durch eine konstante Vermehrungsrate modelliert. Diese führt zum typischen exponentiellen Wachstum. In vielen Artikeln und Berichten über das Corona Virus wird auf das exponentielle Wachstum Bezug genommen. Diese Annahmen sind identisch mit dem Verhulst-Modell. Neben der Vermehrung sieht die Verhulst-Gleichung zudem eine Reduktion vor, die sich dadurch ergibt, dass Neuansteckungen eben nur dann möglich sind, wenn nicht bereits alle angesteckt sind. Je mehr Personen bereits betroffen sind, desto weniger neue Ansteckungen sind möglich. Es ist klar, dass diese Reduktion erst bei hohen Fallzahlen bedeutsam wird. Das Verhulst-Modell ist ein Modell aus dem Lehrbuch und es kann für reale Daten genutzt werden, indem man die für das Modell nötigen Vermehrungsraten aus den Daten schätzt und in die Gleichung einsetzt. Damit die Vorhersage funktioniert, sollten sowohl die Modellannahmen zutreffend, als auch die Daten zuverlässig sein. (Das Verhulst-Modell ist in folgenden Büchern von mir ausführlich dargestellt: Therapeutisches Chaos, Systemische Psychologie, Komplexe Welt).

Mathematik, die auf alles passt: Wenn man nicht über eine fertig mathematische Gleichung für ein Problem verfügt oder dieser nicht raut, kann man auf Gleichungen zurückgreifen, die sich auf alles anpassen lassen. Solche flexiblen Gleichungen sind z.B. Polynome. Je mehr Teilgleichungen ein Polynom enthält, desto besser lässt es sich an beliebige Daten anpassen. Das Polynom sagt inhaltlich nichts aus über die Mechanismen, die ablaufen - diese könnten auch ganz anders aussehen, aber es erlaubt es den jeweiligen Prozess in einer Gleichung einzufangen und nachzubilden. Diese Gleichung kann dann benutzt werden, um auch einige Tage in die Zukunft zu schauen. Ob sie auch dafür geeignet ist zeigt sich aber erst, wenn sie mit den tatsächlichen Daten immer wieder verglichen wird. Ein solches Polynom habe ich für die Corona Fallzahlen in Wien erstellt und gestern bereits dargestellt (siehe unten).

Selbstorganisation:  Beide Möglichkeiten können genutzt werden, um Prognosen zu erstellen. Diese Prognosen beschreiben ein Bild von den Geschehnissen, welches sehr weit entfernt ist vom Schicksal einzelner erkrankter Menschen. Sie gehen davon aus, dass eine Vorhersage der Fallzahlen möglich ist, ohne jede einzelne Person im Detail zu kennen und ohne zu wissen, wen sie wann und wo getroffen hat und noch treffen wird und wie sie diese anderen Personen begrüßt und so weiter. Die Gleichungen beschreiben also ein Bild aus großer Entfernung. Es ist ein Muster auf der Makroebene des Systems. Diese entsteht aus den vielen Einzelschicksalen von Menschen und der unglaublich großen Vielfalt ihrer Verhaltensweisen. Die Ebene der einzelnen Menschen und ihrer Verhaltensweisen wird als Mikroebene eines Systems bezeichnet.

Wenn aus der unermesslichen Vielzahl von Systemelementen und Einflüssen der Mikroebene ein deutlich erkennbares Muster wird, handelt es sich um einen Prozess der Selbstorganisation. Die Einzelteile bringen das Muster der Makroebene hervor, ohne das sie wissen wie sie dazu beitragen. Gleichzeitig ist das entstehende Muster mächtig und zwingt die Einzelteile in seinen Bann. Da es genügt, das Menschen einander begegnen, um das Virus weiterzutragen, ist unbedeutend was sie sonst so tun. Wenn jede erkrankte Person mehr als nur eine weitere ansteckt, dann wird sich das Virus weiter verbreiten. Aus der Vielfalt des Lebens kann im Rahmen einer Epidemie/Pandemie ein erschreckend einfaches und extrem stabiles Muster entstehen. Selbstorganisation ist ein Prozess, der schnell und dramatisch verlaufen kann.

Theorien der Selbstorganisation gehören zu den zentralen Theorien Komplexer Systeme (vgl. Systemische Psychologie). Sie fragen danach, wie aus der Vielfalt an Möglichkeiten ein dominantes Muster hervortritt. Ein solches dominantes Muster lässt sich dann vielleicht in einer Gleichung beschreiben. Aber, es könnte sein, dass jedes System eine etwas andere Gleichung hervorbringt. Die Komplexitätsforschung geht davon aus, dass sich viele Systeme nicht an vorgefertigten einfachen Gleichungen halten.

Die Lösung: Wenn man die Mikroebene des Systems möglichst gut im Computer simuliert, dann kann man das entstehende makroskopische Muster direkt beobachten. Möglicherweise weicht es von den vorgefertigten Gleichungen aus der Literatur stark ab.

Autonome Agenten: Eine seit langen bekannte Methode ist die der Simulation mit Autonomen Agenten. Auch wir von Complexity-Research haben solche Simulationen schon vor ca. 20 Jahren programmiert und genutzt (LINK). Dazu wird ein gigantisches Schachbrettfeld erzeugt. Auf diesem befinden sich - zufällig angeordnet - die autonomen Agenten. Wie viele es sind und wie dicht sie zueinander stehen kann man in der Simulation frei wählen. Die Agenten bewegen sich zufällig von Zeitschritt zu Zeitschritt auf dem Schachbrett und treffen dabei andere Agenten. Diese können sich mit einer vorgewählten Wahrscheinlichkeit gegenseitig anstecken und bewegen sich danach weiter zufällig über das Feld. Nimmt man typische Bewegungsmuster z.B. einer Großstadt als Grundmuster, kann man die dort auftretenden Bewegungen und Begegnungen im Computer nachbilden. Solche Simulationen werden viele hundert mal mit immer neuen Zufallskonstellationen gestartet und die Ergebnisse können gemittelt werden. Solche Modelle sind also nicht darauf angewiesen, dass das makroskopische Muster von Beginn an bekannt ist. Das ist ein großer Vorteil. Hilfreich ist zudem, dass man verschiedene Verhaltensregeln für die simulierten Agenten gegeneinander antreten lassen kann. So kann man sehen ob Maßnahmen wie Schulschließungen - zumindest im Modell - wirksam sind. Simulationen sind aber nur so gut wie die Modellannahmen, die in das Modell einfließen. Es handelt sich um eine virtuelle Welt im Computer und die Passung zur realen Welt stellt ein ernstzunehmendes Problem dar.

Analyse

Komplexe Systeme verhalten sich unvorhersehbar. Das ist es, was sie als komplexe Systeme auszeichnet. Die Verbreitung des Corona-Virus ist hingegen erschreckend einfach vorherzusagen. Solange es nicht gelingt, durch Maßnahmen die Ansteckungsraten zu drücken, folgt die Verbreitung einem simplen exponentiellen Verlauf. Die ungebremste Verbreitung des Corona-Virus zeigt also kein komplexes Verhalten.

Vorhersagemodelle können leicht aus gegebenen Daten bestimmt werden. Dabei scheint es wichtig, nicht ein Modell für ein ganzes Land zu erstellen, sondern lokale Besonderheiten zu berücksichtigen indem lokale Modelle für einzelne Bundesländer oder gar Gemeinden erstellt werden.

Nimmt man etwa die Daten für Wien bis zum 15.03. um ein Modell anzupassen, so können aus diesem Modell Vorhersagen über den weiteren Verlauf getroffen werden. Die Anpassung eines exponentiellen Modells ist einfach und kann im Excel geschehen. Die Fallzahlen bis zum 15.03. werden zunächst logarithmiert. Der exponentielle Verlauf wird damit geradegebogen zu einer linearen Kurve. Für diese kann mit einer einfachen Regression die Steigung bestimmt werden und der weitere logarithmierte Verlauf vorhergesagt werden. Macht man die Logarithmierung dann wieder rückgängig - durch eine Exponentialfunktion - so erhält man die vorhergesagten Fallzahlen.

Für aufwändigere Modelle kann eine andere Software hilfreich sein. GChaos (LINK) erlaubt es Polynome anzupassen, so dass auch Dellen, Abflachungen und kleine Peaks modelliert werden können. Der prognostizierte Kurvenverlauf sieht damit nicht viel anders aus als ein simples exponentielles Modell ist aber eventuell passgenauer.

Für Wien zeigt sich ab dem 16.03. ein vorhergesagter Verlauf der dramatisch ansteigt. Die tatsächlichen Fallzahlen lassen sich damit vergleichen. Ein simpler statistischer Test berechnet zunächst den Unterschied zwischen der vorhergesagten und tatsächlichen Fallzahl. Dieser wird quadriert und durch die vorhergesagte Zahl geteilt. Kommt ein Wert heraus der größer ist als 2,7 so ist die Abweichung statistisch bedeutsam (signifikant). Das Vorgehen ist ein sog. Chi-Quadrat-Test.

Die Fallzahlen für Wien zeigen bisher keine bedeutsamen Abweichung von der Prognose. Das ist nicht gut, aber vielleicht auch kein Wunder - denn die mittlere Inkubationszeit liegt bei 5-6 Tagen und erst danach kann sich eine Wirkung der Maßnahmen zeigen. Sie müsste in den nächsten Tagen deutlich werden.

Die orangenen Punkte wurden für die Modellanpassung benutzt. Die rote Kurve durch diese Punkte wird verlängert. Die blauen Punkte zeigen die tatsächlichen Fallzahlen. Die Daten sind die jeweils gegen 15 Uhr veröffentlichten Zahlen (LINK).