Lorenz-System

Als eines der prominentesten Beispiele für ein chaotisches  System kann das Wetter gelten. So versuchte der Meteorologe Edward Lorenz  1956 eine Analyse zur Wettervorhersage, der er ein relativ einfaches mathematisches Gleichungssystem zu Grunde legte (erschienen ist diese Arbeit von Lorenz 1963). 
Obwohl das mathematische Gleichungssystem das Verhalten dieses theoretischen Systems vollständig determinierte, stieß er zufällig auf einen „Mangel an Vorhersagbarkeit  bei ungenauen Ausgangsbedingungen“ und entdeckte damit ein Verhalten, welches er als Schmetterlingseffekt bezeichnete. 

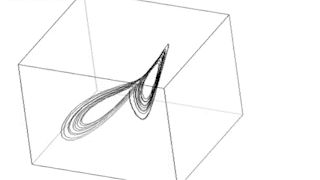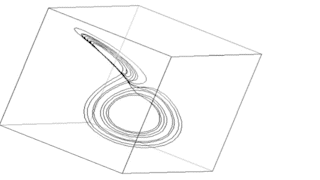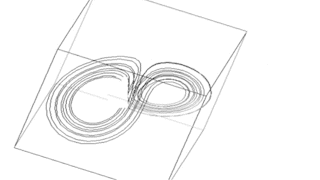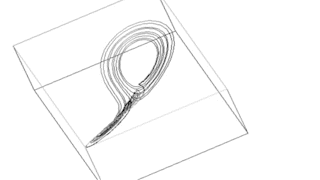
Die Animation (oben) zeigt die Phasenraumdarstellung des von Lorenz benutzten Wettermodells im chaotischen Zustand. Die drei generierenden Gleichungen sind relativ einfach. Sie lauten:  

Hinsichtlich ihrer physikalischen Bedeutung beschreiben die Gleichungen Konvektionsströme, wie sie auch in Flüssigkeiten beobachtet werden können (sog. Bénard-Konvektion). 
Nach Lorenz ist x der Stärke konvektiver Bewegung proportional, z ist ein Maß der Abweichung vom linearen vertikalen Temperaturprofil und y ist proportional zur Temperaturdifferenz zwischen aufsteigenden und abfallenden Strömungen. s, r und b sind Konstanten des Systems, die je nach Zahlenwert entweder zu einfachen regulären Zyklen, zu komplexen Zyklen (Torus) oder zu Chaos führen (Wege ins Chaos). Typische Werte für Chaos sind r = 29, s = 10, b = 8/3. Für nicht zu große r sollen die Gleichungen ein realistisches Modell konvektiver Bewegung darstellen.